I am interested in a variety of topics in the physics of complex quantum systems including topics in Condensed Matter Physics, Quantum Simulation, and Quantum Information. I am currently at the University of Pennsylvania and am co-advised by Professor Martin Claassen and Professor Eugene J. Mele. I am supported by a NSF GRFP Fellowship.
See here for my publications, here for my slides, or below for a description of my research.
Controlling Systems and Engineering Responses in Dissipative Quantum Systems
Every system and object is coupled to its environment and hence to some extent dissipation is relevant for the description of physical properties. In cavities the Q-factor describes this loss of initially coherent oscillation to the environment, while for qubits dissipation and environmental noise are essential challenges to realizing robust quantum computation. A fully quantum description of a system coupled to a memoryless (Markovian) environment is given by the Lindblad formalism which dictates a form of the master equation for the time evolution of the density matrix so that the evolution is completely positive and trace preserving. In recent years, this formalism has seen a great number of applications to spin chains and quantum information systems. Relatively few studies have focused on the physics of quantum materials subject to dissipation and how material properties and responses can be changed by coupling to an environment.
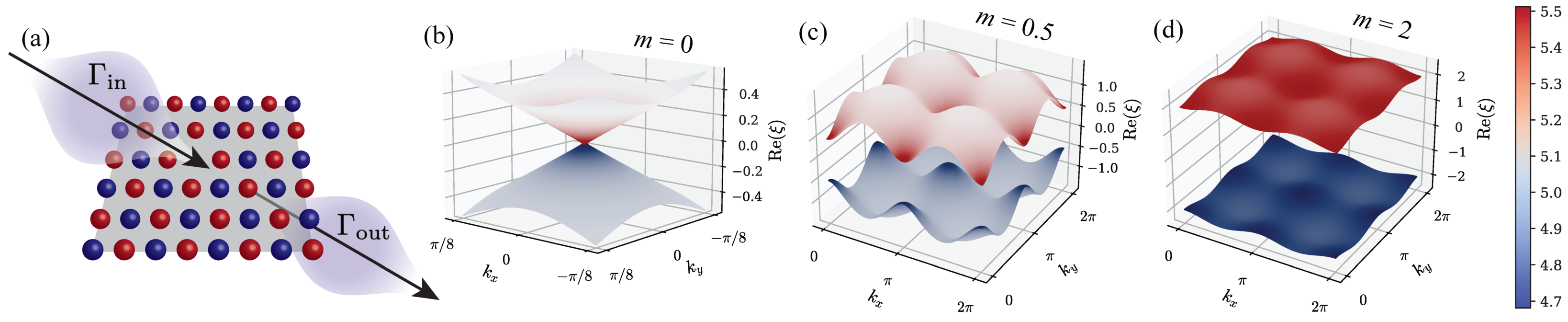
A first application of engineering material properties is to flatten electronic bands using dissipative coupling to an environment. Flat bands are an ideal environment to realize exotic physics such as superconductivity (cuprates have flat bands at the Fermi energy), correlated insulating states (such as those in twisted bilayer graphene), and to study quantum geometric properties (such as Berry curvature effects and superfluid weight bounds). In Phys. Rev. B 106, 161109 (2022), Martin Claassen and I showed that under certain circumstances it is possible for dissipation to induce flat bands in a system with otherwise dispersive bands. Additionally we characterized the symmetries necessary to realize these flat bands and proposed possible materials realizations. A continuing thread of my research is whether it is possible to engineer other material properties using dissipation.
Following up on modulating system properties using dissipation, it is important to understand what measurable response properties will be. To do this, I considered systems that can be described by models that are quadratic in fermions or bosons (which are non-interacting). In this case, one can obtain a “third-quantized” single-particle matrix form for the (Keldysh) Green functions of the system and by Wick’s theorem higher point correlation functions can be evaluated. We then applied this formalism to a variety of response properties in spin chains, bilayer graphene, and bosonic optical lattices. A modulation of atomic density in a bosonic optical lattice is illustrated above where anisotropies in coupling to sublattices leads to a momentum-dependent distribution of particle density. This work is published in npj Quantum Materials 9, 104 (2024).
An ongoing direction of my research is studying this generalizes to interacting systems, such as those with Coulomb interaction, or hard-core bosons such as qubit systems. To do this I have considered theoretical approaches such as perturbative expansions in terms of Feynman diagrams, and computational methods using matrix product operators and tensor-network based algorithms.
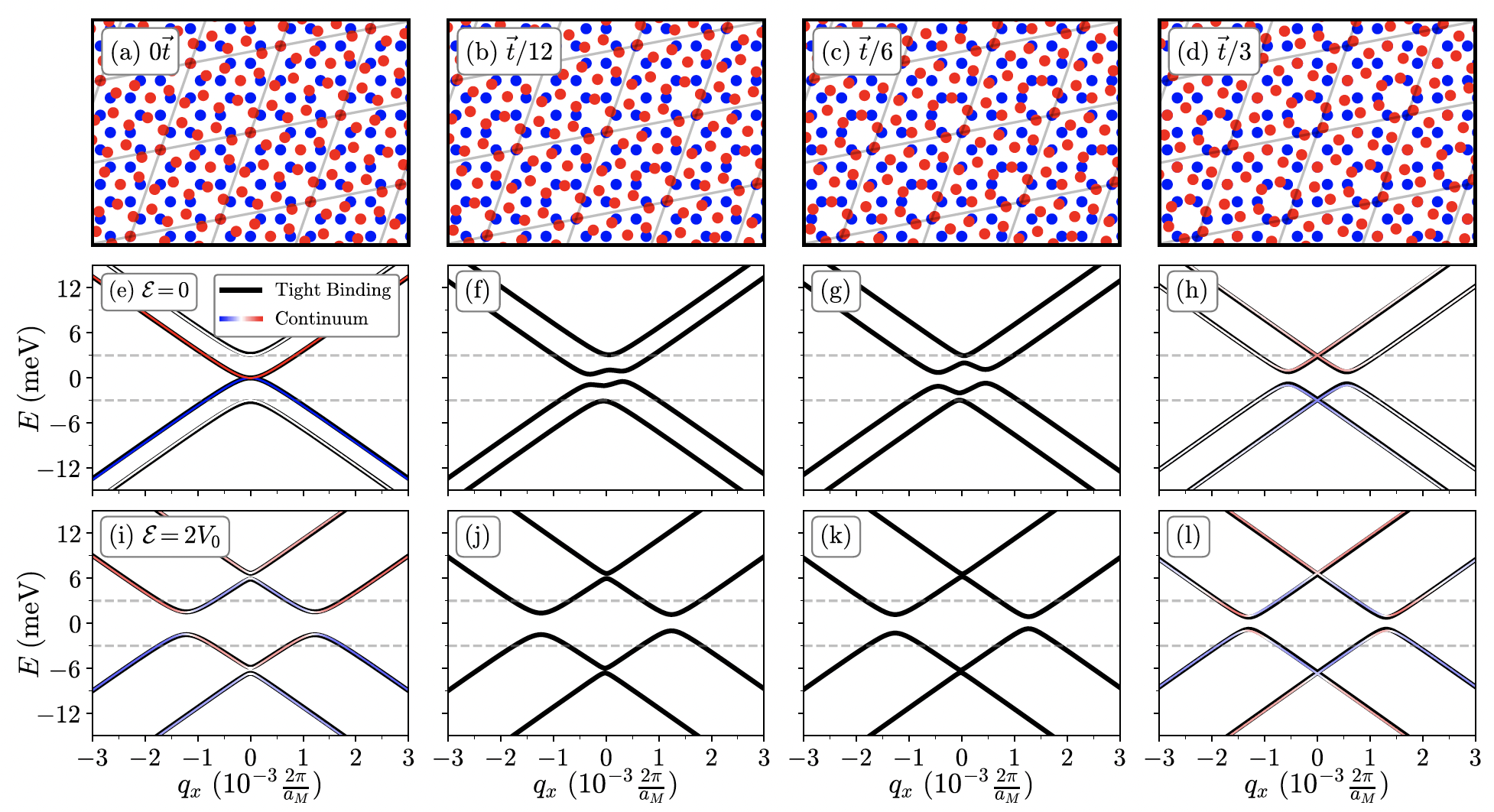
Over the last decade, moiré materials have emerged as a platform to realize electronic physics at an energy scale much smaller than that of conventional metals and insulators. This means that interactions become important for describing the relevant physics as typified by the 2018 discovery of superconductivity in “magic-angle” twisted bilayer graphene. On the way to these low energy structures at small twist angles that exhibit strongly renormalized band structures are large twist angle commensurate structures. These large angle structures exhibit many of the same features as the untwisted structures, but at a much lower energy scale that is conducive for electron-electron interactions and electron-phonon interactions becoming relevant.
Inspired by this guiding principle, I studied the electronic and optical properties of commensurate twisted bilayer graphene. It was known before that there are AB stacking like and AA stacking like structures where the AA structure is gapped. I quantitatively studied this gap and showed that it vanishes exponentially with decreasing twist angle. This gap is important because in the small region of momentum space about the gap the quantum geometry changes rapidly between that of two disjoint layer Dirac fermions. This varying geometry leads to surprisingly large optical responses and in particular surprisingly large circular dichroism which occurs from the natural optical activity of a time-reversal symmetric system. My work is documented in Phys. Rev. B 107, 041408 (2023) and Phys. Rev. B 108, 085421 (2023).
I studied this question under the tutelage of Professor Rahul Roy by using studying large scale tight-binding at and network models. I found that for various distributions of disorder: white noise, gaussian noise, Poissonian noise, and power-law spatially correlated noise the critical exponents obtained were independent of the disorder distribution. This indicates that the IQHE universality class includes many possible and reasonable disorder distributions.
Two references regarding this question are: EPL 13, 453 (1990), and Pramana 58, 271 (2002).
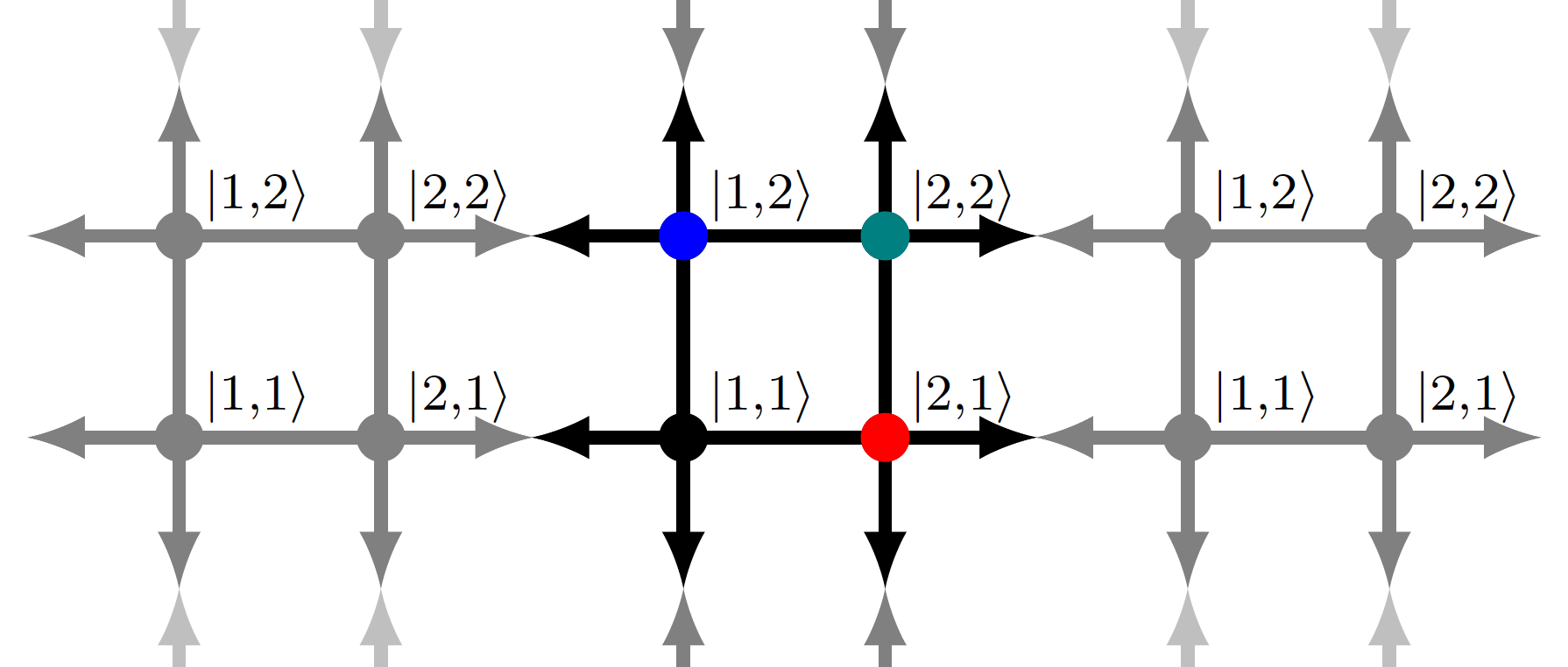
To complete these studies of plateau transitions, which are a type of localization transition, I used tight-binding and network models. Tight-binding are a central class of theoretical models which describe electronic band structures in terms of collections of isolated orbitals. Tunnelings between orbitals are then introduced and the conductivity of the system may then be computed. Network models on the other hand focus on scattering at nodes and phase accumulation between nodes. A central result in the theory of localization is that in the presence of time-reversal symmetry (TRS), in two dimensions any disorder localizes all states Phys. Rev. Lett 42, 673 (1979). However, this theorem does not apply to systems that break TRS where the tunnelings have complex phases as is the case in Chern insulators and the IQHE.
The computational exploration of metal-insulator transitions is very computationally expensive. This is largely due to the magnitude of the transition: insulators have a very short characteristic length, while conductors have a very long characteristic length. For example, while considering 10 orbitals may be sufficient to describe an insulating phase, 100000 or more orbitals may be needed to accurately determine the conductivity of a metallic phase. To overcome this computational cost, I developed an efficient code based on transfer matrix methods and recursive Green’s function methods to quickly determine the localization length, and thus conductivity, for a given tight-binding (or network) model. In particular, I used this code it to gain insight into localization transitions in topological materials through:
- Reexamining previous results with greater computational power
- Studying the critical behavior of systems in symmetry classes whose phase transitions have not been investigated
- Studying new (disordered) models that break symmetries as parametrized by a continuous parameter
One publication that resulted from this work is Phys. Rev. B 105, 045144 (2022).
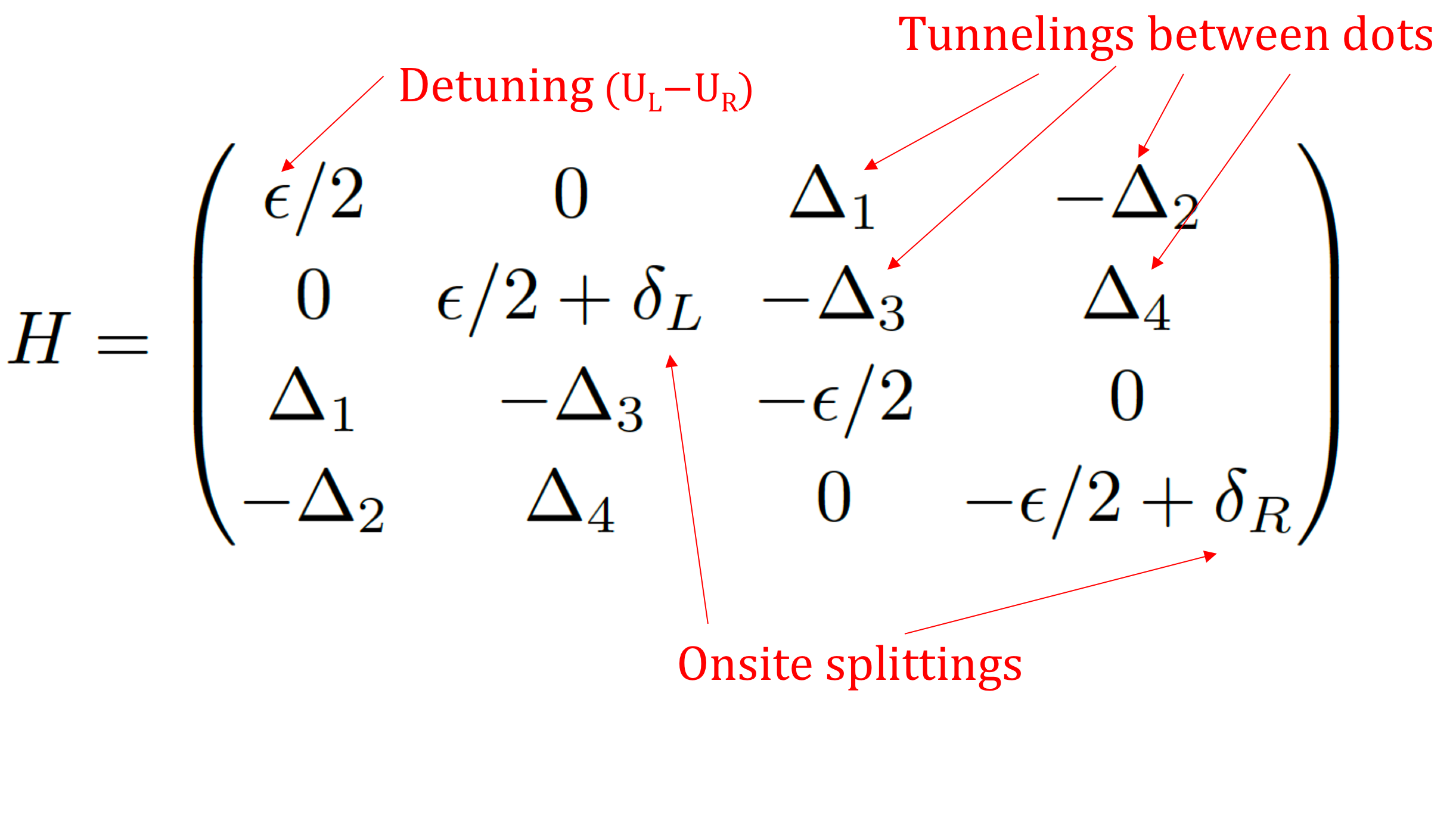
Qubits are in principle one of the simplest quantum systems, consisting of two observable states. However, real qubits are never completely isolated from the environment and often have additional degrees of freedom. Specifically, semiconductor quantum dots are a leading approach for the implementation of solid-state based quantum computing. For charge based semiconductor quantum dot qubits, the observable is position on a “left” or “right” dot. However, with two quantum dots, there are not necessarily two states: the band structure real solids (such as silicon) contain additional pseudospin (or “valley”) states that form additional onsite states.
A “charge-tunneling” Hamiltonian may be formed from the outer product of these charge states, with onsite energies and tunneling frequencies determined from experimental results. The charge-tunneling Hamiltonian is able to predict and explain many, but not all experimental results. In particular, Professor HongWen Jiang’s group has experimentally discovered two novel behaviors that I have shown cannot be explained using a charge-tunneling Hamiltonian. This means that there are physical mechanisms or degrees of freedom that have not been included. I have worked on identifying these mechanisms.

For example, coherent oscillations of the wavefunction between states emerge naturally in any system with tunneling. However, when considering variations on the time-dependence of driven qubit systems near experimental parameters, I observed a secondary interference pattern known as the Landau-Zener Interference Pattern. In addition, I have observed additional interference results that I believe are novel and have worked on developing a quantitative model.
Two references regarding this question are: Phys. Rev. B 92, 205431 (2015), and arXiv:1101.5852 (2011).
In concert to explictating observed physical properties of these qubits, the fundamental units of quantum computing, I have developed and implemented an efficient numerical algorithm to evaluate the time evolution of these systems.
In quantum information, density matrices are the standard method to simulate the evolution of driven quantum systems. Often, unitary evolution may be used instead. This is of practical use because unitary evolution can be optimized to be much faster than density matrix evolution. In particular, I developed three practicable optimization techniques:
- evolution through intervals with a constant Hamiltonian in one step (Floquet method)
- storage of repeated time-dependent features (Piecewise Floquet method)
- iterative extension of previous computations (Recursive method)
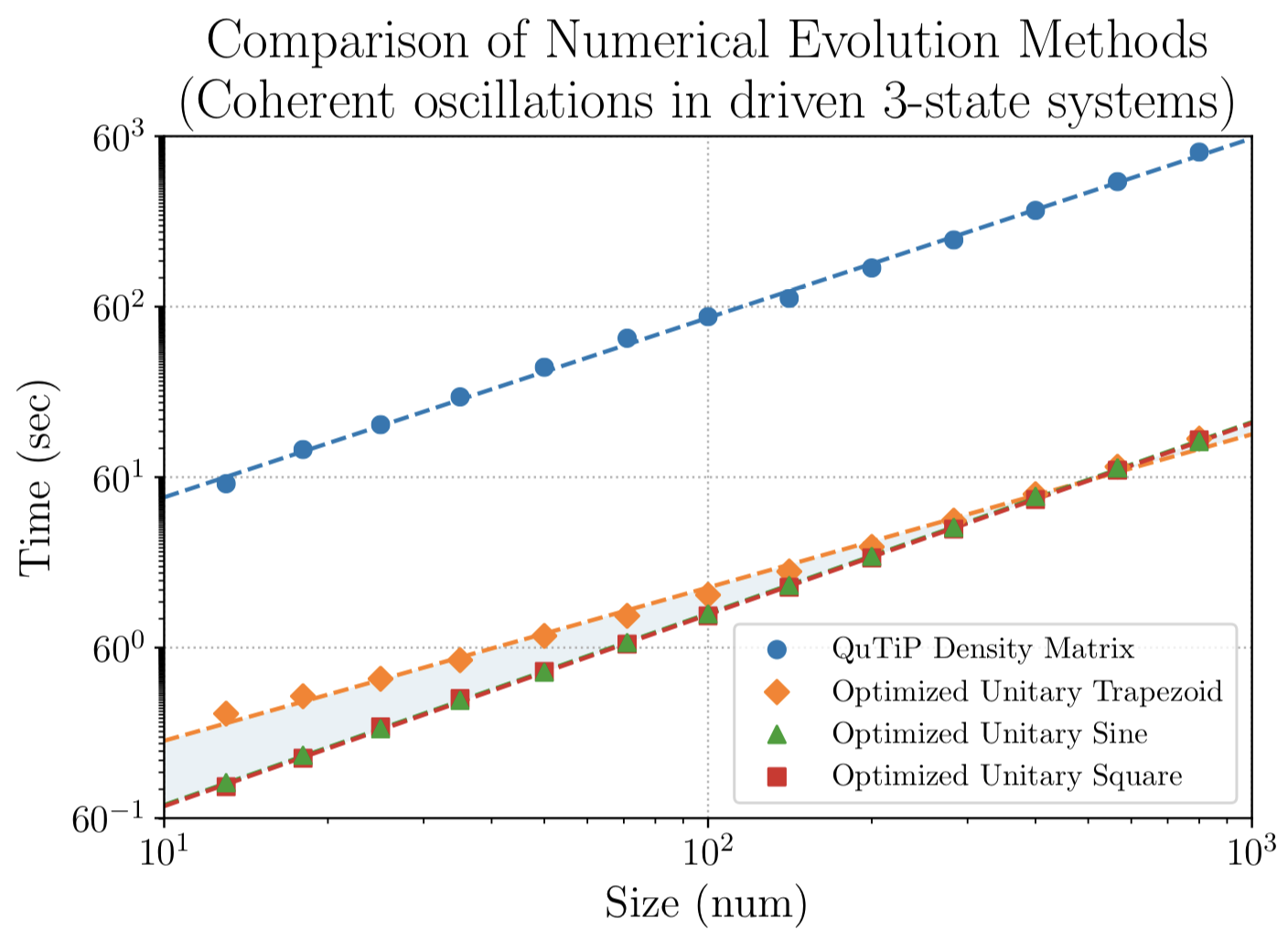
For a driven four-state system, my unitary evolution technique is two orders of magnitude faster than the corresponding density matrix evolution as implemented in QuTiP. The plot above shows the time to simulate various driven quantum systems, and assumes the best-case scenario for QuTiP, and the worst case scenario for the unitary methods.
See J. Phys. Commun. 4, 055004 (2020) for more details.